KD_K

Likelihood and Maximum Likelihood Estimation

Likelihood

While probability answers the question, "Given the model, what is the chance of seeing this data?", likelihood tells us, "How well does a model explain a set of observed data?" In other words, likelihood quantifies how plausible the observed data is under the assumption that the model is correct.

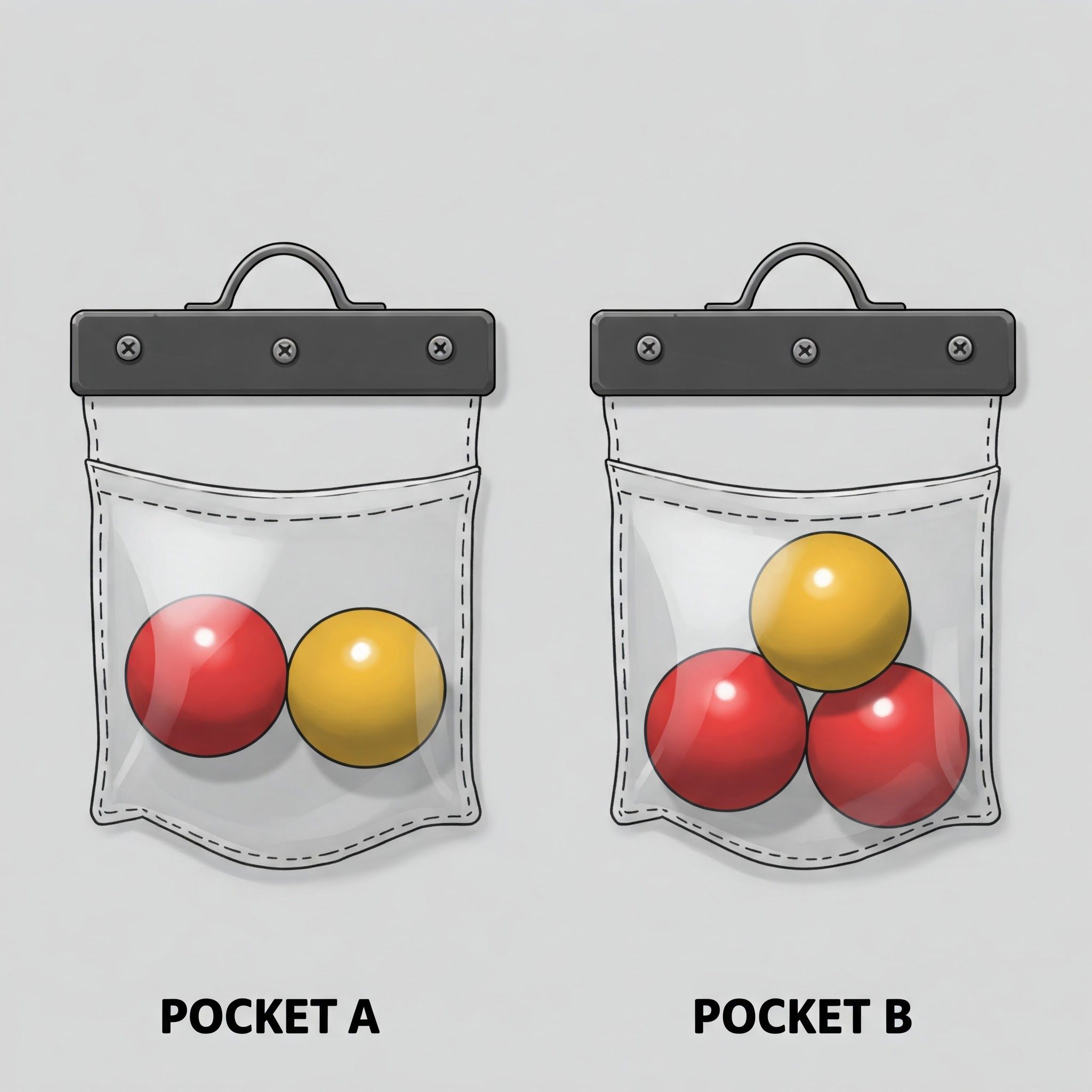
pockets for understanding likelihood and probability

In pocket A, the probability of drawing a red ball is $P(R|A) = {1\over 2}$, and the probability of drawing a yellow ball is $P(Y|A) = {1\over 2}$. In pocket B, the probability of drawing a red ball is $P(R|B= {2\over 3})$, and the probability of drawing a yellow ball is $P(Y|B)= {1\over 3}$.

These are conditional probabilities, meaning that for each pocket, the probabilities sum to 1.

However, if we consider the problem from the perspective of the balls instead, this represents likelihood. For example, if we have already drawn a red ball, from which pocket is this ball likely to have come? Likelihood allows us to infer what is behind the observation—where the ball came from. Unlike probability, likelihood does not necessarily sum to 1, as the likelihood function is not treated as a probability distribution over the pockets($P(R|A)+P(R|B) >1$). Instead, likelihood is a function of the pockets, with the observed balls held constant.

Mathematically, if we denote the observed data as $ X $ and the parameters of a model as $ \Theta $, the likelihood function $ L $ is written as:

$$ L(\Theta | X) = P(X | \Theta) $$

Here, $ P(X | \Theta) $ represents the probability of the observed data $ X $ given the parameters of the model $ \Theta $.

Maximum Likelihood Estimation (MLE)

From the example above, guessing the pocket from which the ball was drawn is analogous to Maximum Likelihood Estimation (MLE).

An Intuitive Example of MLE

Let's say you've recently developed a crush on someone and want to know if they feel the same way. You start initiating conversations, sending messages like What are you doing this weekend?, Do you like coffee?, and How’s your day? However, your crush only responds every other day. Based on this observed behavior, you want to estimate whether they are interested in you or not.

This scenario can be framed as an MLE problem:

Mathematically, we estimate:

$$ P(\text{Response frequency} | \text{Crush's interest level}) $$

Given the observed responses, we infer which underlying "model" (crush's interest level) best explains the data. The most likely explanation is the one that maximizes the likelihood function.

Formal Definition of MLE

More formally, MLE is written as:

$$ \hat{\theta} = \arg\max_{\theta} L(\theta | X) $$

Where we estimate the model parameters $ \Theta $ that maximize the likelihood function $ L $ given the observed data $ X $.

Reference

MLE explanation video @hyukppen